
En 1777, el naturalista y matemático francés Buffon analizó un sencillo pero interesante problema, conocido actualmente como la Aguja de Buffon, de cuyo resultado se extrae una forma de calcular el número pi mediante probabilidad geométrica.
Se trata de lanzar una aguja sobre un papel en el que se han trazado rectas paralelas distanciadas entre sí de manera uniforme. Se puede demostrar que si la distancia entre las rectas es igual a la longitud de la aguja, la probabilidad de que la aguja cruce alguna de las líneas es 2/pi. Esto es, para determinar pi, tras N tiradas de aguja, siendo A el número de veces que la aguja ha cruzado alguna línea, se calculará pi = 2N/A (aprox).
Para ver una demostración gráfica (www.metablake.com) del experimento, pulsa aquí.
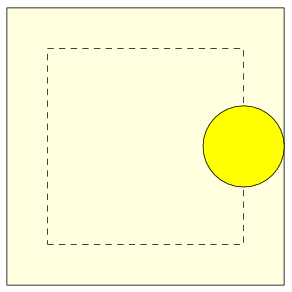
Otro problema relacionado es el de determinar, para una moneda de diámetro D, en un tablero con cuadrículas de lado L, la probabilidad de que dicha moneda, lanzada sobre el tablero, caiga completamente dentro de alguna casilla. Buffon trataba de hacer un juego simple en el que la apuesta fuese justa.
De la figura superior, queda claro, midiendo las superficies del cuadrado exterior y el interior, que la probabilidad de que la moneda caiga dentro del cuadrado es P = ((L-D)/L)^2. De aquí, para que la apuesta sea justa, P = 1/2 , es necesario que D sea aproximadamente 0.29 veces L.
La pregunta subyacente es la siguiente: ¿qué relación tendrá que existir entre la longitud de la aguja (l) y la separación de las rectas (d) en el primer problema para que lanzar una aguja sea una apuesta justa?
Para más información (fuentes e imágenes):
Clean Tile Problem (Weisstein, E.W., from Mathworld).
Buffon's Needle Problem (Weisstein, E.W., from Mathworld).




3 comentarios:
La apuesta justa del juego de la moneda de Buffon se basa, al igual que el de la aguja, en probabilidad geométrica, y en ambos casos aparecen números irracionales (raíz de 2 en la moneda y pi en la aguja).
Según las fuentes citadas en la entrada, si x=l/d, entonces P(x)=2x/pi, por lo que sería necesario espaciar las líneas paralelas pi/4 veces la longitud de la aguja para obtener un juego de apuesta justa.
Sin embargo, dado que se trata de relaciones basadas en números irracionales, nunca seremos capaces de crear un juego de apuesta justa, puesto que siempre estaremos aproximando dichos números.
Lapsus blogae: es 4/pi veces, es decir, aproximadamente 1.27.
Como bien dice JAF, nunca una apuesta puede ser justa. Me alegra que matemáticos y poetas, sigan la misma senda. :)
Sin-Son
Publicar un comentario